Le Système International d'unités (SI) trouve son origine en France peu après la Révolution française de 1789. Ce système décimal basé sur la définition du mètre puis du kilogramme a permis l'utilisation d'unités communes dans les échanges commerciaux et les sciences. Ce système a continué de se développer au fil du temps pour finalement aboutir en 1960, lors de la 11ème Conférence Générale des Poids et Mesures (CGPM), à un système de six unités de base auxquelles viendra plus tard s'ajouter la mole, unité de quantité de matière, en 1971.
En 1974 le Luxembourg adopte pour la première fois officiellement le Système International d’unités (SI) dans le Règlement grand-ducal du 22 mai 1974 portant application de la directive 71/354/CEE du 18 octobre 1971 concernant le rapprochement des législations des Etats membres relatives aux unités de mesure.
Ce règlement a été ensuite remplacé par le Règlement grand-ducal du 14 octobre 1981 modifié portant application de la directive 80/181/CEE du 20 décembre 1979 concernant le rapprochement des législations des Etats membres relatives aux unités de mesure. Aujourd’hui c’est ce Règlement grand-ducal modifié qui est toujours d’application.
Le Système International (SI) est un système de sept unités qui sont à la base de toutes les grandeurs officiellement utilisées actuellement dans le monde entier par les 39 états associés à la CGPM et les 56 états signataires de la Convention du Mètre.
Unités de base du SI
En 2018, la 26ème Conférence Générale des Poids et Mesures a redéfini lessept unités de base du Système international d'unités (SI), sur la base de constantes de la physique fondamentale.
Les unités de base du système international sont les « unités indépendantes » (ou « unités fondamentales ») à partir desquelles sont obtenues par analyse dimensionnelle toutes les autres unités, dites « unités dérivées ».
Le tableau ci-dessous présente les unités SI de base (Source BIPM) :
Grandeur de base |
Unité SI de base |
||
| Nom | Symbole | Nom | Symbole |
| Longueur | l, x, r, etc. | mètre | m |
| Masse | M | kilogramme | kg |
| Temps, durée | T | seconde | s |
| Courant électrique | I, i | ampère | A |
| Température thermodynamique | T | kelvin | K |
| Quantité de matière | N | mole | mol |
| Intensité lumineuse | Iv | candela | cd |
Unités SI dérivées cohérentes avec noms et symboles particuliers
Certaines unités dérivées cohérentes du SI ont reçu des noms spéciaux, par souci de simplification. Il est important de souligner que chaque grandeur physique n’a qu’une seule unité SI cohérente, même si cette unité peut être exprimée sous différentes formes au moyen de noms spéciaux ou de symboles particuliers. L’inverse, toutefois, n’est pas vrai ; la même unité SI peut, dans certains cas, être employée pour exprimer les valeurs de plusieurs grandeurs différentes.
Par exemple, la combinaison particulière des unités de base m2 kg s–2 a reçu le nom spécial joule, symbole J, quand elle est l’unité d’une énergie.
Par définition J =m2 kg s–2
Le tableau ci-dessous présente des exemples d'unités SI dérivées cohérentes dont le nom et le symbole comprennent des unités SI dérivées cohérentes ayant des noms spéciaux et des symboles particuliers :
| Unité SI dérivée cohérente | |||
| Grandeur dérivée | Nom | Symbole | Expression en unités SI de base |
| Viscosité dynamique | pascal seconde | Pa s | m–1 kg s–1 |
| Moment d'une force | newton mètre | N m | m2 kg s–2 |
| Tension superficielle | newton par mètre | N/m | kg s–2 |
| Vitesse angulaire | radian par seconde | rad/s | m m–1 s–1 = s–1 |
| Accélération angulaire | radian par seconde carrée | rad/s2 | m m–1 s–2 = s–2 |
| Flux thermique surfacique, éclairement énergétique | watt par mètre carré | W/m2 | kg s–3 |
| Capacité thermique, entropie | joule par kelvin | J/K | m2 kg s–2 K–1 |
| Capacité thermique massique, entropie massique | joule par kilogramme kelvin | J/(kg K) | m2 s–2 K–1 |
| Energie massique | joule par kilogramme | J/kg | m2 s–2 |
| Conductivité thermique | watt par mètre kelvin | W/(m K) | m kg s–3 K–1 |
| Energie volumique | joule par mètre cube | J/m3 | m–1 kg s–2 |
| Champ électrique | volt par mètre | V/m | m kg s–3 A–1 |
| Charge électrique volumique | coulomb par mètre cube | C/m3 | m–3 s A |
| Charge électrique surfacique | coulomb par mètre carré | C/m2 | m–2 s A |
| Induction électrique, déplacement électrique | coulomb par mètre carré | C/m2 | m–2 s A |
| Permittivité | farad par mètre | F/m | m–3 kg–1 s4 A2 |
| Perméabilité | henry par mètre | H/m | m kg s–2 A–2 |
| Energie molaire | joule par mole | J/mol | m2 kg s–2 mol–1 |
| Entropie molaire, capacité thermique molaire | joule par mole kelvin | J/(mol K) | m2 kg s–2 K–1 mol–1 |
Exposition (rayons x et  ) ) |
coulomb par kilogramme | C/kg | kg–1 s A |
| Débit de dose absorbée | gray par seconde | Gy/s | m2 s–3 |
| Intensité énergétique | watt par stéradian | W/sr | m4 m–2 kg s–3 = m2 kg s–3 |
| Luminance énergétique | watt par mètre carré stéradian | W/(m2 sr) | m2 m–2 kg s–3 = kg s–3 |
| Concentration d'activité catalytique | katal par mètre cube | kat/m3 | m–3 s–1 mol |
Unités cohérentes dérivées
Les unités dérivées sont formées à partir de produits de puissances des unités de base. Les unités dérivées sont définies comme le produit de puissances des unités de base. Quand le produit des puissances ne comprend pas de facteur numérique autre que 1, les unités dérivées sont appelées unités dérivées cohérentes. Les unités de base et les unités dérivées cohérentes du SI forment un ensemble cohérent, désigné sous le nom d'ensemble cohérent des unités SI. Le mot cohérent est utilisé ici dans le sens suivant : lorsque l'on utilise des unités cohérentes, les équations reliant les valeurs numériques des grandeurs prennent exactement la même forme que les équations reliant les grandeurs proprement dites. Ainsi, si l'on utilise uniquement des unités d'un ensemble cohérent, on n'a jamais besoin de facteurs de conversion entre les unités.
Les grandeurs utilisées dans le domaine scientifique sont en nombre illimité ; il n'est donc pas possible de fournir une liste complète des grandeurs et unités dérivées.
Le tableau ci-dessous présente un certain nombre d'exemples de grandeurs dérivées, avec les unités dérivées cohérentes correspondantes exprimées directement en fonction des unités de base (Source BIPM) :
| Grandeur dérivée | Unité SI dérivée cohérente | ||
| Nom | Symbole | Nom | Symbole |
| Superficie | A | mètre carré | m2 |
| Volume | V | mètre cube | m3 |
| Vitesse | 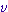 |
mètre par seconde | m/s |
| Accélération | A | mètre par seconde carrée | m/s2 |
| Nombre d'ondes | 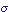 , ,  |
mètre à la puissance moins un | m–1 |
| Masse volumique | 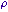 |
kilogramme par mètre cube | kg/m3 |
| Masse surfacique |
|
kilogramme par mètre carré | kg/m2 |
| Volume massique | V | mètre cube par kilogramme | m3/kg |
| Densité de courant | J | ampère par mètre carré | A/m2 |
| Champ magnétique | H | ampère par mètre | A/m |
| Concentration de quantité de matière (a), concentration | C | mole par mètre cube | mol/m3 |
| Concentration massique | 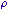 , , 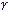 |
kilogramme par mètre cube | kg/m3 |
| Luminance lumineuse | Lv | candela par mètre carré | cd/m2 |
| Indice de réfraction (b) | n | un | 1 |
| Perméabilité relative (b) | 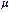 r r |
un | 1 |
| (a) | Dans le domaine de la chimie clinique, cette grandeur est aussi appelée concentration de matière. |
| (b) | Ce sont des grandeurs sans dimension, ou grandeurs de dimension un. Le symbole « 1 » pour l'unité (le nombre « un ») n'est généralement pas mentionné lorsque l'on précise la valeur des grandeurs sans dimension. |
Unités cohérentes dérivées particulières
Par souci de commodité, certaines unités dérivées cohérentes ont reçu un nom spécial et un symbole particulier. Elles sont au nombre de vingt-deux et sont mentionnées dans le tableau ci-dessous. Ces noms spéciaux et ces symboles particuliers peuvent eux-mêmes être utilisés avec les noms et les symboles d'autres unités de base ou dérivées pour exprimer les unités d'autres grandeurs dérivées.
Le tableau ci-dessous présente les unités SI dérivées cohérentes ayant des noms spéciaux et des symboles particuliers :
Unité SI dérivée cohérente (a) |
||||
| Grandeur dérivée | Nom | Symbole | Expression utilisant d'autres unités SI | Expression en unités SI de base |
| Angle plan | radian (b) | Rad | 1 (b) | m/m |
| Angle solide | stéradian (b) | sr (c) | 1 (b) | m2/m2 |
| Fréquence | hertz (d) | Hz | s–1 | |
| Force | newton | N | m kg s–2 | |
| Pression, contrainte | pascal | Pa | N/m2 | m–1 kg s–2 |
| Energie, travail, quantité de chaleur | Joule | J | N m | m2 kg s–2 |
| Puissance, flux énergétique | Watt | W | J/s | m2 kg s–3 |
| Charge électrique, quantité d'électricité | coulomb | C | s A | |
| Différence de potentiel électrique, force électromotrice | Volt | V | W/A | m2 kg s–3 A–1 |
| Capacité électrique | Farad | F | C/V | m–2 kg–1 s4 A2 |
| Résistance électrique | Ohm | O | V/A | m2 kg s–3 A–2 |
| Conductance électrique | siemens | S | A/V | m–2 kg–1 s3 A2 |
| Flux d'induction magnétique | Weber | Wb | V s | m2 kg s–2 A–1 |
| Induction magnétique | Tesla | T | Wb/m2 | kg s–2 A–1 |
| Inductance | Henry | H | Wb/A | m2 kg s–2 A–2 |
| Température Celsius | degré Celsius (e) | °C | K | |
| Flux lumineux | Lumen | lm | cd sr (c) | cd |
| Eclairement lumineux | Lux | lx | lm/m2 | m–2 cd |
| Activité d'un radionucléide (f) | becquerel (d) | Bq | s–1 | |
| Dose absorbée, énergie massique (communiquée), kerma | gray | Gy | J/kg | m2 s–2 |
Equivalent de dose, Equivalent de dose ambiant, Equivalent de dose directionnel, Equivalent de dose individuel |
sievert (g) | Sv | J/kg | m2 s–2 |
| Activité catalytique | Katal | kat | s–1 mol | |
| (a) | Les préfixes SI peuvent être utilisés avec n'importe quel nom spécial et symbole particulier, mais dans ce cas l'unité qui en résulte n'est plus une unité cohérente. |
| (b) | Le radian et le stéradian sont des noms spéciaux pour le nombre un, qui peuvent être utilisés pour donner des informations sur la grandeur concernée. En pratique, les symboles rad et sr sont utilisés lorsque c'est utile, et le symbole pour l'unité dérivée « un » n'est généralement pas mentionné lorsque l'on donne les valeurs des grandeurs sans dimension. |
| (c) | En photométrie, on maintient généralement le nom et le symbole du stéradian, sr, dans l'expression des unités. |
| (d) | Le hertz est uniquement utilisé pour les phénomènes périodiques, et le becquerel pour les processus aléatoires liés à la mesure de l'activité d'un radionucléide. |
| (e) | Le degré Celsius est le nom spécial du kelvin utilisé pour exprimer les températures Celsius. Le degré Celsius et le kelvin ont la même taille, ainsi la valeur numérique d'une différence de température ou d'un intervalle de température est identique quand elle est exprimée en degrés Celsius ou en kelvins. |
| (f) | L'activité d'un radionucléide est parfois appelée de manière incorrecte radioactivité. |
| (g) | Voir la Recommandation 2 (CI-2002) du CIPM sur l'utilisation du sievert. |
Règles d’écriture des noms et symboles d’unités et expression des valeurs des grandeurs
Un paragraphe dans la brochure du SI est aussi consacrée aux règles d'écriture des valeurs des grandeurs. Ces règles et conventions ont été décidées et adoptées au fil des réunions sucessives de la CGPM et du CIPM depuis 1889. Ce sont des conventions qui ont été proposées par les pays membres de ces organisations, qui se sont engagés à les respecter.
Le vocabulaire de la métrologie
Le vocabulaire de la métrologie possède aussi ses règles et conventions. Celles-ci sont définies au niveau international dans un document publié par le BIPM : le Vocabulaire International de Métrologie (VIM) (pdf).

